When betting at TrustDice, you have the opportunity to win a jackpot on every roll you make. TrustDice put 7% of the profit they make from their dice game into the jackpot and so the jackpot prize is constantly increasing until it is won. The rules of the jackpot are:
 The rules indicate 2 important facts about the TrustDice jackpot:
The rules indicate 2 important facts about the TrustDice jackpot: - The jackpot prize constantly increases until it is won
- The probability of winning the jackpot always remains the same
These 2 characteristics ensure that sooner or later the jackpot will grow large enough that betting on TrustDice is statistically profitable. We will now calculate how large the jackpot needs to be for this to be the case.
There are 2 methods we can use to find when the jackpot is so big that it’s profitable to bet on it:
- Estimate how many rolls (on average) are required to win the jackpot and then calculate how much it would cost to make that many rolls. If the jackpot is larger than this amount, then the jackpot is profitable.
- Use the formula for expected value to determine what the jackpot needs to be for the expected value to be greater than zero.
Method 1: Estimating the cost of rolling enough times to win
We first need to calculate the probability of winning the jackpot. To win the jackpot requires both of the following:
- You must win the dice roll
- Your jackpot roll must be “7777″
The combined probability of both of these outcomes is:
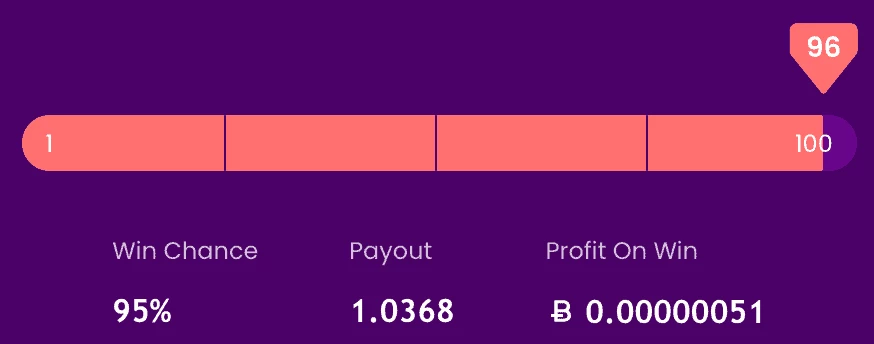
probability_jackpot = probability_dice_roll × probability_7777Since we want to maximize our chance of winning the jackpot, we choose the highest possible “Roll Under” value of 96. This makes
probability_dice_roll = 95%
.
 To calculate the probability of the jackpot roll being “7777″ we observe the probability of any one digit in the jackpot roll being 7 is 10% or 0.1. The probability that all 4 digits are 7 is therefore
To calculate the probability of the jackpot roll being “7777″ we observe the probability of any one digit in the jackpot roll being 7 is 10% or 0.1. The probability that all 4 digits are 7 is therefore
0.1 × 0.1 × 0.1 × 0.1
. The probability of winning the jackpot is therefore:
probability_jackpot = 0.95 × 0.1 × 0.1 × 0.1 × 0.1 = 0.000095This means the expected number of rolls to win the jackpot is:
rolls = 1 / probability_jackpot = 10526.316When we select “roll under 96″ we have a 95% chance of winning
1.0368 × bet_amount
. So, on average, each bet will cost:
bet_cost = bet_amount - 0.95 × 1.0368 × bet_amount = 0.01504 × bet_amountSo the expected cost of rolling enough times to win the jackpot is:
cost = 10526.316 × 0.01504 × bet_amount = 158.316 × bet_amountWinning the jackpot will return a prize of:
win = 0.8 × (bet_amount / max_bet_amount) × jackpotWe want to find the jackpot amount that makes
win > cost
. This means:
0.8 × (bet_amount / max_bet_amount) × jackpot > 158.316 × bet_amountDividing each side of the inequality by
0.8 × bet_amount / max_bet_amount
yields:
jackpot > 158.316 × max_bet_amount / 0.8
jackpot > 197.895 × max_bet_amountPutting in the
max_bet_amount = 0.5 BTC
we get:
jackpot > 98.947 BTCSo if the jackpot is 98.947 BTC or larger it is profitable to bet at TrustDice.
Method 2: Finding where the expected value is positive
The formula for expected value is:
EV = PD × PJ × S × J + PD × W × B - B
PD : Probability that the dice roll wins
PJ : Probability that the jackpot roll wins
S : Share of the jackpot that the bettor will win
J : Size of the jackpot
W : Payout multiplier if the dice roll wins
B : Bet amountPicking the highest probability of winning the dice roll makes
PD = 0.95
and
W = 1.0368
. The jackpot share is
0.8 × B / Bmax
. The probability of winning the jackpot roll is
PJ = 0.14
. Plugging these numbers into the formula for expected value gives:
EV = 0.95 × 0.1⁴ × 0.8 × B / Bmax × J + 0.95 × 1.0368 × B - B
= 0.000076 × B / Bmax × J - 0.01504 × BWe want to find where
EV > 0
:
0.000076 × B / Bmax × J - 0.01504 × B > 0
0.000076 × B / Bmax × J > 0.01504 × B
J > 0.01504 × B / (0.000076 × B / Bmax)
J > 197.895 × BmaxThe TrustDice rules indicate
Bmax = 0.5 BTC
and so we have:
J > 98.947 BTCSo as long the jackpot is at least 98.947 BTC the expected value of betting is greater than zero and so betting is profitable.
Deciding how much to bet
Now we know how high the jackpot must be for betting to be profitable, the next question is how much to bet on each roll. To qualify for the jackpot you must bet at least 0.001 BTC and the maximum allowed bet is 0.5 BTC so you will want to bet within this range. We can show that the bet amount doesn’t actually impact the return on investment:
ROI = EV / B × 100%
= (0.000076 × B / Bmax × J - 0.01504 × B) / B × 100%
= 0.0152 × J - 1.504So if the jackpot is 100 BTC your expected ROI from a single bet is 0.8% whether you bet 0.001 BTC or 0.5 BTC or anything in between. However, assuming you are going to need to bet 10,526.316 times to win the jackpot, it will make a big difference in how much capital you will need and what total profit you can expect:
capital = 158.316 × B
profit = 0.8 × B / Bmax × J - 158.316 × B
return_on_capital = profit / capital × 100%If the jackpot is 100 BTC we would have:
| Bet per roll | Required capital | Profit | Return on Capital |
|---|---|---|---|
| 0.001 BTC | 0.158 BTC | 0.002 BTC | 1.64% |
| 0.01 BTC | 1.583 BTC | 0.017 BTC | 1.64% |
| 0.1 BTC | 15.832 BTC | 0.168 BTC | 1.64% |
| 0.5 BTC | 79.158 BTC | 0.842 BTC | 1.64% |
The profit in the table above assumes you stop betting after winning the jackpot but if you were to bet 0.001 BTC, hitting the jackpot would earn you 0.16 BTC and leave 99.84 BTC still in the jackpot. This means the jackpot is still profitable so you could keep betting and win the jackpot again and again. Under this model betting 0.001 BTC is no different than betting 0.5 BTC except you would need much less capital.
However, if we assume there are multiple people competing for the jackpot then perhaps you would want to bet big so that when you win the jackpot you take a larger share of it before other players have a chance to win it.
Summary
It feels a bit disappointing that you can “win” a huge 100 BTC jackpot and you only get 0.16 BTC. This leaves 99.84% of the jackpot behind. Usually, if it’s said you “won” something that does not mean you won 0.16% of it.
“I won a million dollar lotto!”
“Wow, are you going to buy a house?”
“Well I won $1,600″…
But this is the structure TrustDice has gone with and it gives this jackpot hunt some interesting characteristics. Do compare this to our writeup of the Nitrogen Jackpot, which is sometimes +EV to bet for and our writeup of the chance of winning the Prime Dice jackpot.

Vlad Hategan
Author
In my career, I wrote for companies like Daily Coin or Crypto Banter while also writing social media content for a number of projects - including NFTs and tokens.
More by Vlad Hategan




